Diffblue Cover for Java
Achieve quality faster with Agentic AI
Diffblue Cover automates unit testing, empowering dev teams to deliver high-quality software faster, efficiently and more reliably than coding assistants or writing tests manually.
Automatically generate unit tests
Diffblue Cover augments developers by automating away tedious and time-consuming aspects of the Java unit and regression testing process.
Accelerates Java unit test creation
Writes comprehensive human readable unit tests that test the actual behavior of your code, including edge cases and scenarios developers may not know to test.
Updates and maintains unit tests after each code change
Diffblue Cover has a deep understanding of how your code works and knows what tests need to be added and updated for every code change. It implements the necessary updates automatically, ensuring coverage doesn’t dip.
Documents your code
Unit tests created describe every behavior of every method – effectively documenting your code, increasing understandability and making future code changes quicker.
Regression detection and impact measurement
Creates tests that reflect the current behavior of your code enabling developers to catch regressions as early as possible and to quickly understand the impact of code changes locally and during the CI process.
Enables rapid coverage increases
Creates unit tests in bulk, covering all relevant branches to rapidly improve coverage and enable teams to reach and maintain coverage goals.
Provides feedback on best testability & coding practices
Suggests and automates code fixes that improve the understandability of Java code and makes it more testable.
One platform,
many capabilities
100% autonomous AI-driven Java unit test generation
Cover autonomously creates an entire unit test suite for your entire application. Cover Core automatically writes and maintains human-like JUnit or TestNG unit tests that are comprehensive, compile, run and accurately validate code behavior
Smart targeted unit testing
Cover Optimize speeds up the time required to run Java unit tests by running only the tests in your project that are relevant to your code change. This minimizes the time needed to run unit tests locally and in CI. Cover Optimize automatically selects only the unit tests required to fully validate that a code change hasn’t introduced regressions; slashing test execution time to accelerate development cycles and increase team productivity.
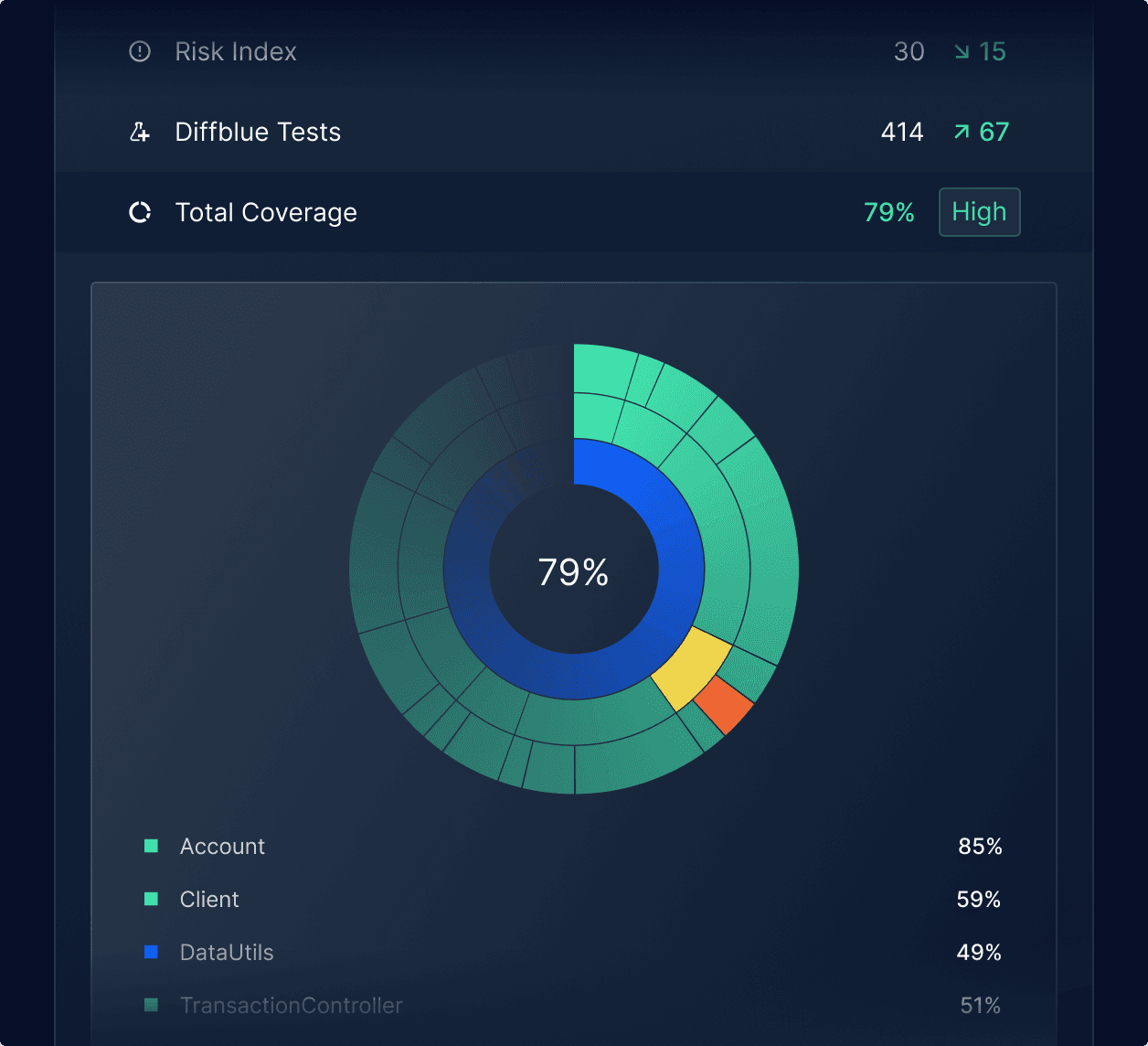
Visualize code coverage and quality reporting
Cover Reports provides reporting and vizualization insight for teams into the state of unit testing in terms of coverage levels, coverage risk, testability and pinpoints actionable insights that improve code quality.
Compare
Diffblue Cover vs Coding Assistants
Works how you work
For Developers
Your AI unit test pilot — the best way to unit test
Leverage the power of AI to generate comprehensive, smart and efficient unit and regression tests to validate each code change you make.
Ready to up your code quality game?
Start unit testing with Diffblue Cover. Increase test coverage, speed up development, and improve application quality.
